线性回归算法梳理

机器学习的一些概念

监督学习、非监督学习、半监督学习的区别

监督学习、非监督学习和半监督学习区别就是训练数据是否拥有标签信息

监督学习：给出了数据及数据的标准答案来训练模型。Regression回归问题、classification分类问题都是典型的监督学习

非监督学习：给了一组数据，但没有给出数据的标签信息，需要从数据中去发现数据间隐藏的结构信息。聚类问题是典型的非监督学习

半监督学习：给出了大量没有标签的数据和少量拥有标签的数据训练模型

过拟合、欠拟合、泛化能力

欠拟合：模型没有很好的捕捉到数据特征，不能够很好的拟合数据

过拟合：模型把训练数据学的“太好了”，导致把数据中的潜在的噪声数据也学到了，测试时不能很好的识别数据，模型的泛化能力下降。

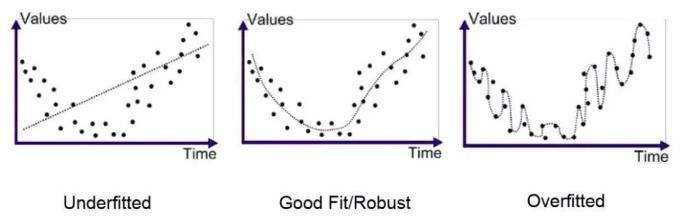
泛化能力**：训练的模型适用于新样本的能力，称为“泛化”能力，具有强范化能力的模型能很好的适用于整个样本空间

线性回归的原理

线性回归遇到的问题一般是这样的。我们有 $m$ 个样本，每个样本对应于 $n$ 维特征和一个结果输出，如下：

$(x^{(0)}_1,x^{(0)}_2,\dots x^{(0)}_n,y^{(0)}),\dots (x^{(m)}_1,x^{(m)}_2,\dots x^{(m)}_n,y^{(m)})$

我们的问题是，对于一个新的 $(x^{(x)}_1,x^{(x)}_2,\dots x^{(x)}_n)$ , 他所对应的 $y^{(x)}$是多少呢？如果这个问题里面的 $y$ 是连续的，则是一个回归问题，否则是一个分类问题。

对于 $n$ 维特征的样本数据，如果我们决定使用线性回归，那么对应的模型是这样的：

$h_θ(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+\dots +\theta_nx_n$

其中 $\theta_i(i = 0,1,2\dots n)$ 为模型参数，$x_i (i = 0,1,2\dots n)$ 为每个样本的 $n$ 个特征值。这个表示可以简化，增加一个特征 $x_0=1$ ，这样 $h_θ(x_1,x_2,…x_n)=\sum_{i=0}^n\theta_ix_i$。

进一步用矩阵形式表达更加简洁如下：

$h_\theta(X)=X\theta$

其中，假设函数 $h_\theta(X)$ 为 $m1$ 的向量,$θ$ 为 $n1$ 的向量，里面有 $n$ 个代数法的模型参数。$X$ 为 $m*n$ 维的矩阵。$m$ 代表样本的个数，$n$ 代表样本的特征数。

得到了模型，我们需要求出需要的损失函数，一般线性回归我们用均方误差作为损失函数。损失函数的代数法表示如下：

$J(\theta_0,\theta_1,\dots ,\theta_n)=\sum_{i=0}^m(h_θ(x_0,x_1,\dots,x_n)−y_i)^2$

进一步用矩阵形式表达损失函数：

$J(\theta)=\frac{1}{2}(X\theta−Y)^T(X\theta−Y)$

线性回归损失函数、代价函数、目标函数

损失函数：$\left| y_i-f(x_i) \right|$ ，一般是针对单个样本 i

代价函数：$1/N.\sum_{i=1}^{N}{\left| y_i-f(x_i) \right|}$ , 一般是针对总体

目标函数：带有正则项的代价函数

优化方法

梯度下降法

沿着梯度下降的方向来求出损失函数的极小值。梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x)求导 = 0的根。牛顿法最大的特点就在于它的收敛速度很快。

拟牛顿法

拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。

线性回归的评估指标

平均绝对误差（MAE）

$MAE=\frac{1}{n}\sum_{i=1}^n|y_i-f_i|$

均方误差（MSE）

$MSE=\frac{1}{n}\sum_{i=1}^n(y_i-f_i)^2$

方均根差（RMSE）

$RMSE = \sqrt{MSE}$

平均绝对百分比误差（MAPE）

$MAPE=\frac{100}{n}\sum_{T=1}^n|\frac{y_i-f_i}{y_i}|$

　R平方

$r^2 = 1-\frac{SS_{res}}{SS_{tot}} = 1-\frac{\sum(y_i-f_i)^2}{\sum(y_i-\overline{y})^2}$

sklearn参数详解

函数：

1	sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

fit_intercept：布尔值。指定是否需要计算线性回归中的截距，即b值。如果为False,那么不计算b值。
normalize：布尔值。如果为False，那么训练样本会进行归一化处理；当为True的时候，则回归量X将在回归之前通过减去平均值并除以I2范数来归一
copy_X：布尔值。如果为True，会复制一份训练数据。
n_jobs：一个整数。任务并行时指定的CPU数量，如果取值为-1则使用所有可用的CPU。
coef_：权重向量
intercept_：截距b值