RNN的结构
RNN结构
DNN以及CNN在对样本提取特征的时候,样本与样本之间是独立的,而有些情况是无法把每个输入的样本都看作是独立的,比如基于时间的序列,因此单纯的DNN和CNN解决这类问题就比较棘手。此时RNN就是一种解决这类问题很好的模型。
一个简单的循环神经网络如图所示,它由输入层、一个隐藏层和一个输出层组成:
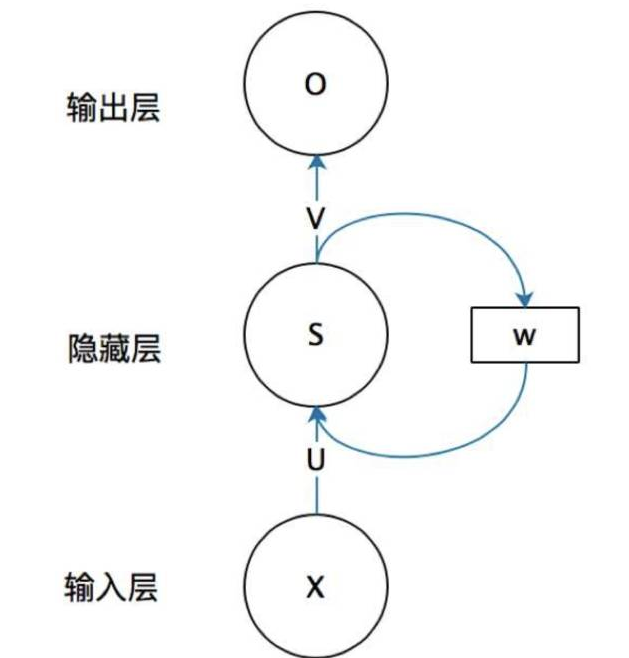
循环神经网络的隐藏层的值 $s$ 不仅仅取决于当前这次的输入 $x$,还取决于上一次隐藏层的值 $s$。权重矩阵 $W$ 就是隐藏层上一次的值作为这一次的输入的权重。
抽象图对应的具体图:
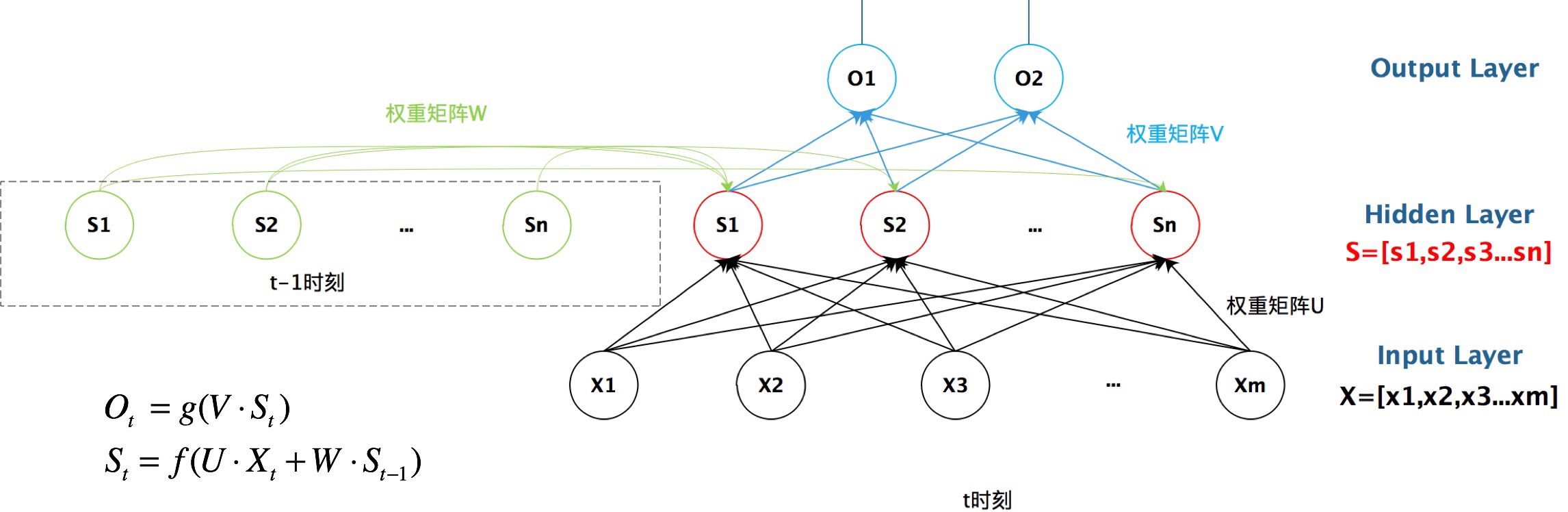
从上图就能够很清楚的看到,上一时刻的隐藏层是如何影响当前时刻的隐藏层的。
把上面的图展开,循环神经网络也可以画成下图:
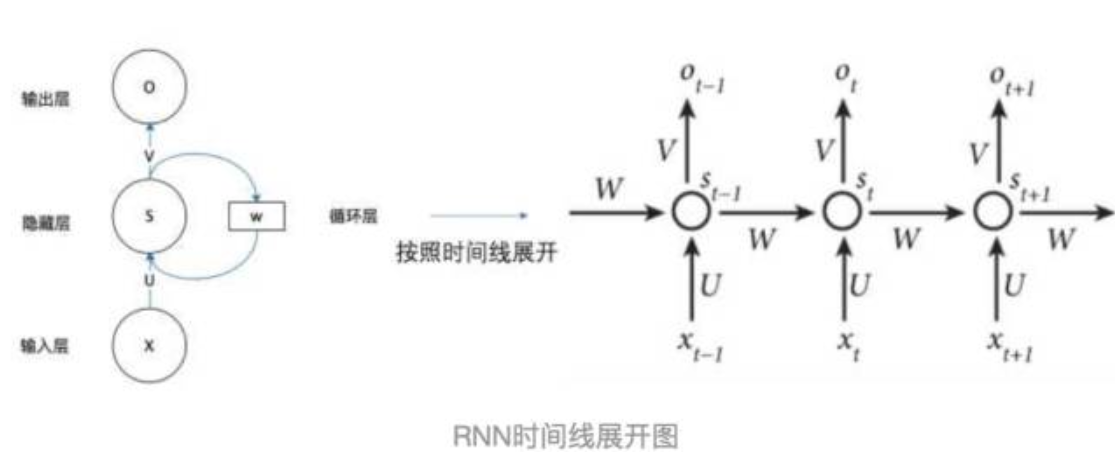
由上图可以看出,RNN的结构是一个重复的过程,且权重 W,U,V 是共享的,这也是借鉴了CNN的思想,可以减少参数量,从而减少计算的复杂度。第 t 时刻隐藏层的输出需要 t-1 时刻的隐藏层的输出,RNN以此来实现信息的传递。
循环神经网络的计算公式:
$S_t$ 的值不仅取决于 $X_t$,还取决于 $S_{t-1}$
RNN反向传播算法推导
RNN反向传播算法的思路和DNN是一样的,即通过梯度下降法一轮轮的迭代,得到合适的RNN模型参数$U,W,V,b,c$。由于我们是基于时间反向传播,所以RNN的反向传播有时也叫做BPTT(back-propagation through time)。当然这里的BPTT和DNN也有很大的不同点,即这里所有的$U,W,V,b,c$在序列的各个位置是共享的,反向传播时我们更新的是相同的参数。
为了找出模型最好的参数 $U,W,V$,就要知道当前参数得到的结果怎么样,因此就要定义损失函数,用交叉熵损失函数:
其中 $y_t$ 是 $t$ 时刻的标准答案,是一个只有一个是$1$,其他都是$0$的向量;$\hat y_t$是预测的结果,与$y_t$的维度一样,但它是一个概率向量,里面是每个词出现的概率。因为对结果的影响,肯定不止一个时刻,因此需要把所有时刻的造成的损失都加起来:
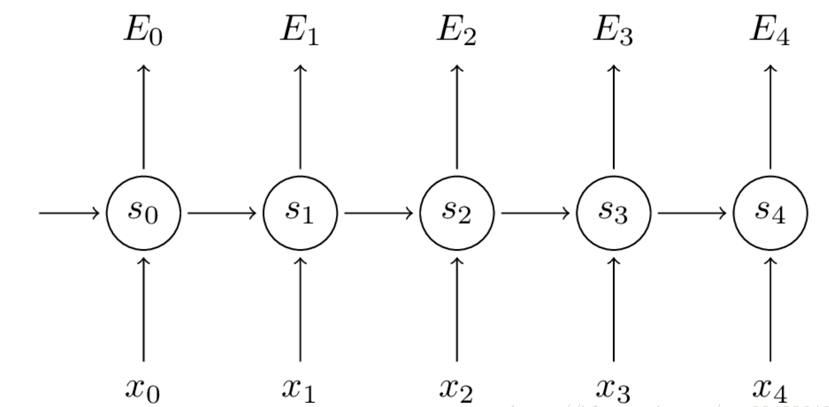
接下来根据损失函数利用SGD来求解最优参数,在CNN中使用反向传播BP算法来求解最优参数,但在RNN就要用到BPTT,它和BP算法的本质区别,也是CNN和RNN的本质区别:CNN没有记忆功能,它的输出仅依赖与输入,但RNN有记忆功能,它的输出不仅依赖与当前输入,还依赖与当前的记忆。这个记忆是序列到序列的,也就是当前时刻受到上一时刻的影响。
因此,在对参数求偏导的时候,对当前时刻求偏导,一定会涉及前一时刻。
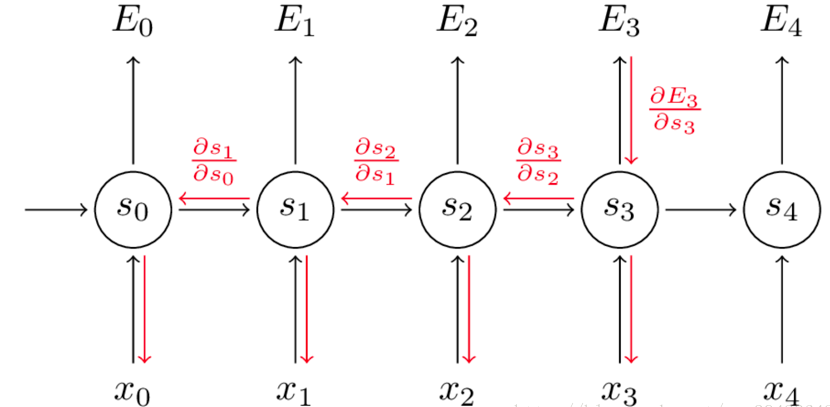
假设我们对 $E_3$ 的 $W$ 求偏导:它的损失首先来源于预测的输出$\hat y_3$,预测的输出又是来源于当前时刻的记忆 $s_3$,当前的记忆又是来源于当前的输出和截止到上一时刻的记忆:$s_3=tanh(Ux_3+Ws_2)$
因此,根据链式法则可以有:
但是,你会发现,$s_2=tanh(Ux_2+Ws_1)$,也就是 $s_2$ 里面的函数还包含了$W$,因此,这个链式法则还没到底,就像图上画的那样,所以真正的链式法则是这样的:
要把当前时刻造成的损失,和以往每个时刻造成的损失加起来,因为每一个时刻都用到了权重参数 $W$。和以往的网络不同,一般的网络,比如人工神经网络,参数是不同享的,但在循环神经网络,和CNN一样,设立了参数共享机制,来降低模型的计算量。
RNN出现的问题
根据上面部分推出的公式:
继续往下展开有:
注意到:$S_t = f(UX_t+WS_{t-1}+b) $,上式的每个偏导其实是一个Jacobian式。
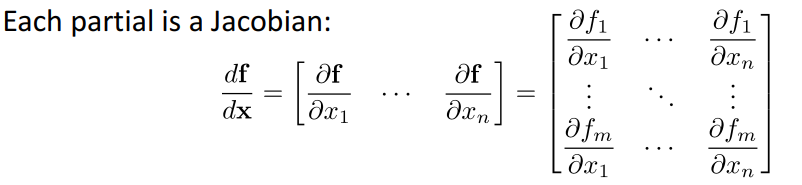
考虑Jacobians的范数,令:
其中,$\beta w,\beta h$ 表示正则化的上界。
将上式回代到连乘的式子得:
这里得 $t$ 表示 time-step,也就是序列越长 $t$ 会越大,即就变成了长期依赖的问题。注意到 $(\beta_w \beta_h)^{t-k}$ 这项其实与矩阵的 $W$ 的初始化有关,假设初始化一些非常小的数,$W$ 的范数也会变得很小,也就是 $\beta_w$ 会变得比较小,那么随着 $t$ 的增长,这一指数项会趋近于 $0$ 而导致梯度消失;相反,如果初始化成为大于1的数,则随着t的增长,会导致*梯度爆炸。
双向RNN
在经典的循环神经网络中,状态的传输是从前往后单向的。然而,在有些问题中,当前时刻的输出不仅和之前的状态有关系,也和之后的状态相关。这时就需要双向RNN(BiRNN)来解决这类问题。例如预测一个语句中缺失的单词不仅需要根据前文来判断,也需要根据后面的内容,这时双向RNN就可以发挥它的作用。
双向RNN是由两个RNN上下叠加在一起组成的。输出由这两个RNN的状态共同决定。
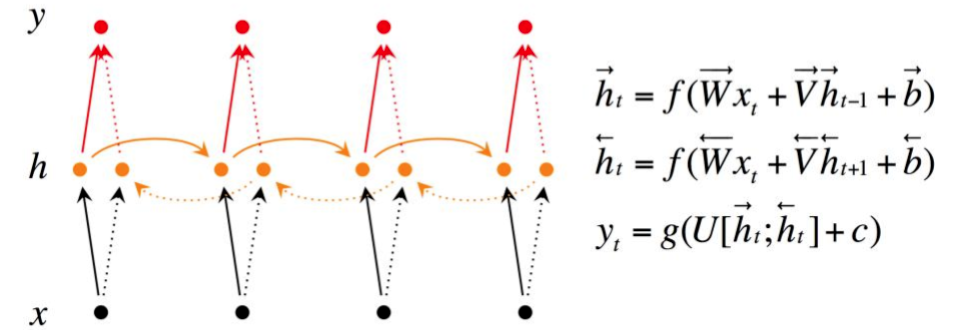
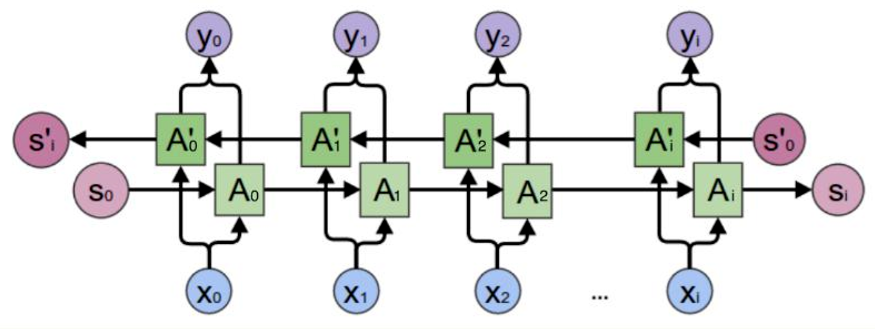
从上图可以看出,双向RNN的主题结构就是两个单向RNN的结合。在每一个时刻 $t$,输入会同时提供给这两个方向相反的RNN,而输出则是由这两个单向RNN共同决定(可以拼接或者求和等)。
递归神经网络
因为神经网络的输入层单元个数是固定的,因此必须用循环或者递归的方式来处理长度可变的输入。循环神经网络实现了前者,通过将长度不定的输入分割为等长度的小块,然后再依次的输入到网络中,从而实现了神经网络对变长输入的处理。一个典型的例子是,当我们处理一句话的时候,我们可以把一句话看作是词组成的序列,然后,每次向循环神经网络输入一个词,如此循环直至整句话输入完毕,循环神经网络将产生对应的输出。如此,我们就能处理任意长度的句子了。
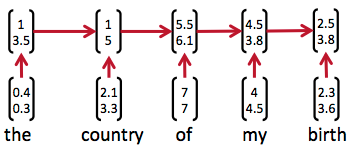
然而,有时候把句子看做是词的序列是不够的,比如下面这句话『两个外语学院的学生』:
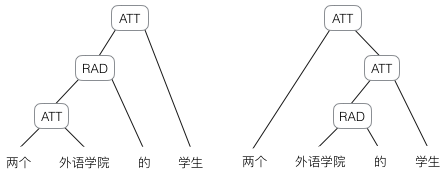
上图显示了这句话的两个不同的语法解析树。可以看出这句话有歧义,不同的语法解析树则对应了不同的意思。为了能够让模型区分出两个不同的意思,我们的模型必须能够按照树结构去处理信息,而不是序列,这就是递归神经网络的作用。当面对按照树/图结构处理信息更有效的任务时,递归神经网络通常都会获得不错的结果。
递归神经网络可以把一个树/图结构信息编码为一个向量,也就是把信息映射到一个语义向量空间中。这个语义向量空间满足某类性质,比如语义相似的向量距离更近。也就是说,如果两句话(尽管内容不同)它的意思是相似的,那么把它们分别编码后的两个向量的距离也相近;反之,如果两句话的意思截然不同,那么编码后向量的距离则很远。如下图所示:
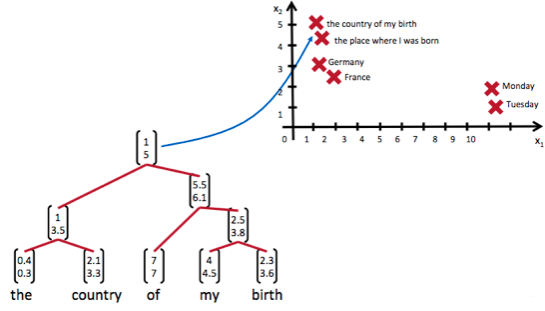
从上图我们可以看到,递归神经网络将所有的词、句都映射到一个2维向量空间中。句子『the country of my birth』和句子『the place where I was born』的意思是非常接近的,所以表示它们的两个向量在向量空间中的距离很近。另外两个词『Germany』和『France』因为表示的都是地点,它们的向量与上面两句话的向量的距离,就比另外两个表示时间的词『Monday』和『Tuesday』的向量的距离近得多。这样,通过向量的距离,就得到了一种语义的表示。
上图还显示了自然语言可组合的性质:词可以组成句、句可以组成段落、段落可以组成篇章,而更高层的语义取决于底层的语义以及它们的组合方式。递归神经网络是一种表示学习,它可以将词、句、段、篇按照他们的语义映射到同一个向量空间中,也就是把可组合(树/图结构)的信息表示为一个个有意义的向量。比如上面这个例子,递归神经网络把句子”the country of my birth”表示为二维向量[1,5]。有了这个『编码器』之后,我们就可以以这些有意义的向量为基础去完成更高级的任务(比如情感分析等)。
如下图所示,递归神经网络在做情感分析时,可以比较好的处理否定句,这是胜过其他一些模型的:
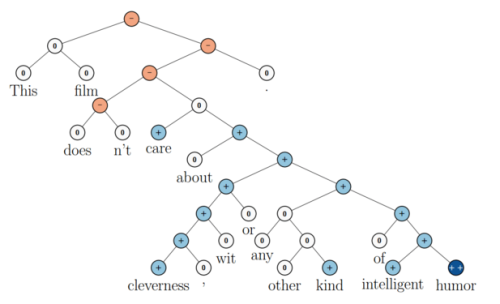
在上图中,蓝色表示正面评价,红色表示负面评价。每个节点是一个向量,这个向量表达了以它为根的子树的情感评价。比如”intelligent humor”是正面评价,而”care about cleverness wit or any other kind of intelligent humor”是中性评价。可以看到,模型能够正确的处理doesn’t的含义,将正面评价转变为负面评价。
尽管递归神经网络具有更为强大的表示能力,但是在实际应用中并不太流行。其中一个主要原因是,递归神经网络的输入是树/图结构,而这种结构需要花费很多人工去标注。如果用循环神经网络,可以直接把句子作为输入。然而,如果用递归神经网络处理,必须把每个句子标注为语法解析树的形式,要花费非常大的精力。很多时候,相对于递归神经网络能够带来的性能提升,这个投入是不太划算的。
LSTM
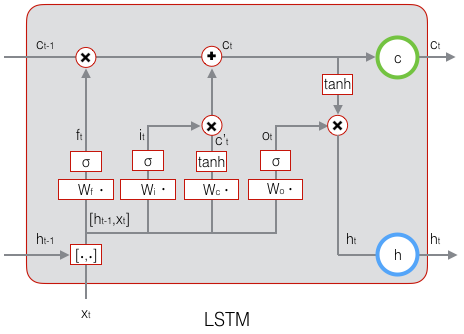
长短时记忆网络(Long Short Term Memory Network, LSTM)的思路比较简单。原始RNN的隐藏层只有一个状态,即$h$,它对于短期的输入非常敏感。假如我们再增加一个状态,即$c$,让它来保存长期的状态,那么问题就解决了。如下图所示:
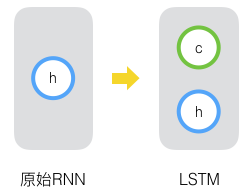
新增加的状态c,称为单元状态(cell state)。我们把上图按照时间维度展开:
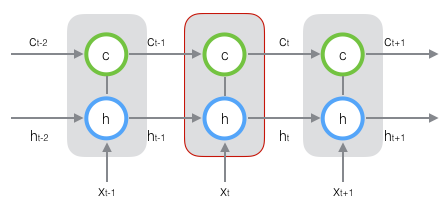
可以看出,在 $t$ 时刻,LSTM的输入有三个:当前时刻网络的输入值 $x_t$、上一时刻LSTM的输出值 $h_{t-1}$、以及上一时刻的单元状态 $c_{t-1}$;LSTM的输出有两个:当前时刻LSTM输出值 $h_t$、和当前时刻的单元状态 $c_t$。注意 $x、h、c$ 都是向量。
LSTM的关键,就是怎样控制长期状态 $c$。在这里,LSTM的思路是使用三个控制开关。第一个开关,负责控制继续保存长期状态 $c$;第二个开关,负责控制把即时状态输入到长期状态 $c$;第三个开关,负责控制是否把长期状态 $c$ 作为当前的LSTM的输出。
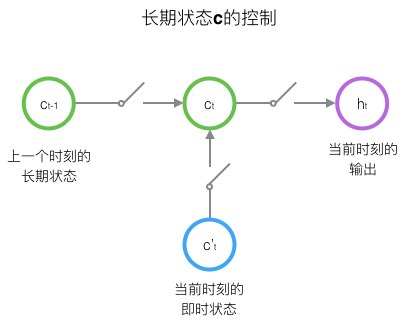
LSTM的前向计算
前面描述的开关是怎样在算法中实现的呢?这就用到了门(gate)的概念。门实际上就是一层全连接层,它的输入是一个向量,输出是一个$0$到$1$之间的实数向量。假设$W$是门的权重向量,$b$是偏置项,那么门可以表示为:
门的使用,就是用门的输出向量按元素乘以我们需要控制的那个向量。因为门的输出是$0$到$1$之间的实数向量,那么,当门输出为$0$时,任何向量与之相乘都会得到$0$向量,这就相当于都不能通过;输出为$1$时,任何向量与之相乘都不会有任何改变,这就相当于都可以通过。因为 $\sigma$ (也就是sigmoid函数)的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c的内容,一个是遗忘门(forget gate),它决定了上一时刻的单元状态 $c_{t-1}$ 有多少保留到当前时刻 $c_t$;另一个是输入门(input gate),它决定了当前时刻网络的输入 $x_t$ 有多少保存到单元状态 $c_t$。LSTM用输出门(output gate)来控制单元状态 $c_t$有多少输出到LSTM的当前输出值 $h_t$。
先来看遗忘门:
上式中,$W_f$ 是遗忘门的权重矩阵,$[h_{t-1},x_t]$ 表示把两个向量连接成一个更长的向量,$b_f$ 是遗忘门的偏置项,$\sigma$ 是sigmoid函数。如果输入的维度是 $d_x$,隐藏层的维度是 $d_h$,单元状态的维度是 $d_c$(通常 $d_c=d_h$),则遗忘门的权重矩阵 $W_f$ 维度是 $d_c \times (d_h+d_x)$。事实上,权重矩阵 $W_f$ 都是两个矩阵拼接而成的:一个是 $W_{fh}$,它对应着输入项 $h_{t-1}$,其维度为 $d_c \times d_h$;一个是 $W_{fx}$,它对应着输入项 $x_t$,其维度为 $d_c \times d_x$。$W_f$ 可以写为:
下图显示了遗忘门的计算:
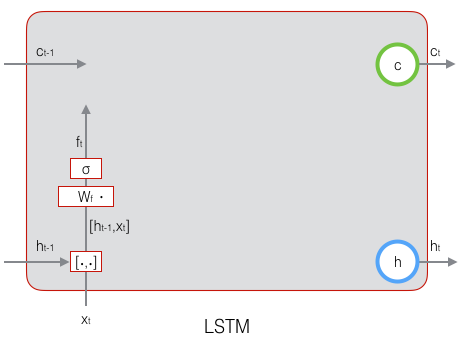
接下来看看输入门:
上式中,$W_i$ 是输入门的权重矩阵,$b_i$ 是输入门的偏置项。下图表示了输入门的计算:
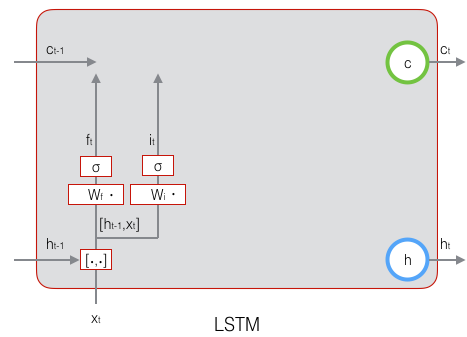
接下来,计算用于描述当前输入的单元状态 $\tilde c_t$,它是根据上一次的输出和本次输入来计算的:
下图表示了 $\tilde c_t$ 的计算:
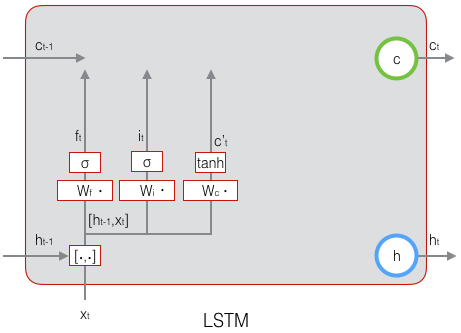
现在,我们计算当前时刻的单元状态 $c_t$。它是由上一次的单元状态 $c_{t-1}$ 按元素乘以遗忘门 $f_t$,再用当前输入的单元状态 $\tilde c_t$ 按元素乘以输入门 $i_t$,再将两个积加和产生的:
符号 $\circ$ 表示按元素乘。下图是 $c_t$ 的计算:
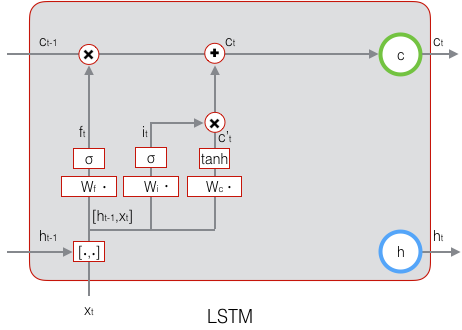
这样,我们就把LSTM关于当前的记忆 $\tilde c_t$ 和长期的记忆 $c_{t-1}$ 组合在一起,形成了新的单元状态 $c_t$ 。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容进入记忆。
下面,我们要看看输出门,它控制了长期记忆对当前输出的影响:
下图表示输出门的计算:
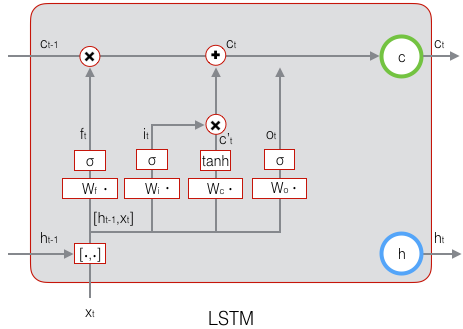
LSTM最终的输出,是由输出门和单元状态共同确定的:
下图表示LSTM最终输出的计算:
GRU
GRU是LSTM网络的一种效果很好的变体,它较LSTM网络的结构更加简单,而且效果也很好,因此也是当前非常流形的一种网络。GRU既然是LSTM的变体,因此也是可以解决RNN网络中的长依赖问题。
在LSTM中引入了三个门函数:输入门、遗忘门和输出门来控制输入值、记忆值和输出值。而在GRU模型中只有两个门:分别是更新门和重置门。具体结构如下图所示:
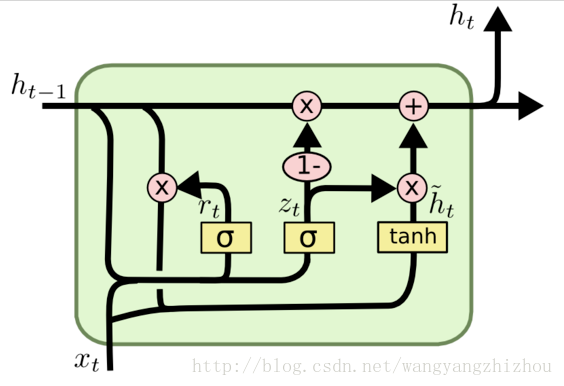
图中的 $zt$ 和 $rt$ 分别表示更新门和重置门。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门控制前一状态有多少信息被写入到当前的候选集 $\tilde h_t$ 上,重置门越小,前一状态的信息被写入的越少。
Text-RNN结构
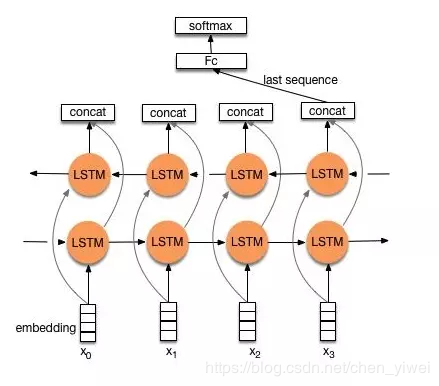
利用Text-RNN模型来进行文本分类。
参考文章
零基础入门深度学习(6) - 长短时记忆网络(LSTM)
RNN中梯度消失和爆炸的问题公式推导
循环神经网络(RNN)原理通俗解释
【直观理解】一文搞懂RNN(循环神经网络)基础篇
零基础入门深度学习(7) - 递归神经网络
基于tensorflow+RNN的新浪新闻文本分类

