卷积运算
卷积运算的定义
我们称 $(f*g)(n)$ 为 $f,g$ 的卷积。
其连续定义为:
其离散定义为:
这两个式子有一个共同的特征:

令 $x=\tau ,y=n-\tau$ ,那么 $x+y=n$ 就是下面这些直线:
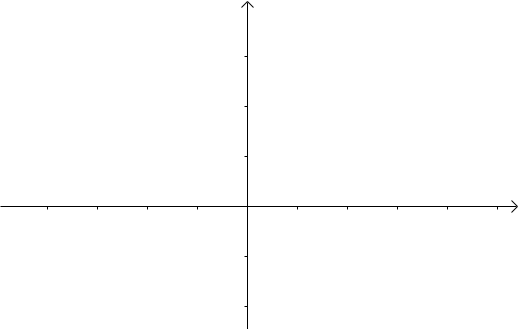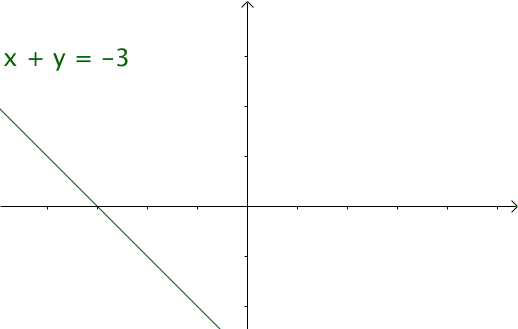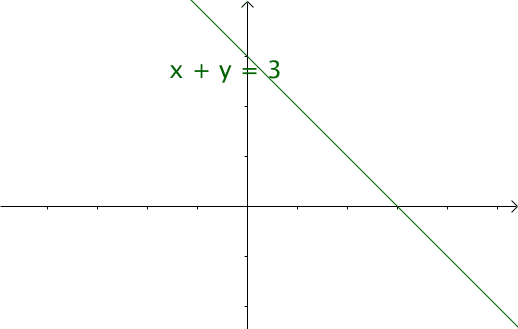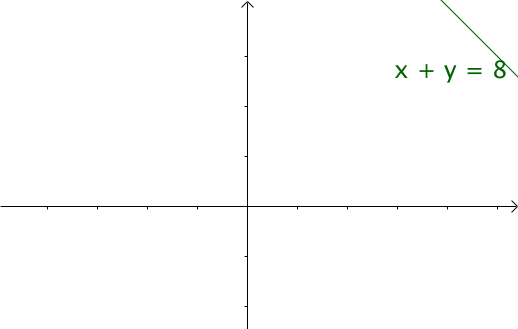
如果遍历这些直线,就好比,把毛巾沿着角卷起来:

离散卷积的例子:丢骰子
假设有两个骰子,点数加起来等于4的概率是多少?

两枚骰子点数加起来为4的概率为:$f(1)g(3)+f(2)g(2)+f(3)g(1)$
符合卷积的定义,把它写成标准的形式就是:$\displaystyle (f*g)(4)=\sum _{m=1}^{3}f(4-m)g(m)$
连续卷积的例子:做馒头
假设馒头的生产速度是 $f(t)$ ,那么一天后生产出来的馒头总量为:$\int _{0}^{24}f(t)dt$
馒头生产出来之后,就会慢慢腐败,假设腐败函数为 $g(t) $,比如,10个馒头,24小时会腐败:$10*g(t)$
想想就知道,第一个小时生产出来的馒头,一天后会经历24小时的腐败,第二个小时生产出来的馒头,一天后会经历23小时的腐败。
如此,我们可以知道,一天后,馒头总共腐败了:$\int _{0}^{24}f(t)g(24-t)dt$
这就是连续的卷积。
卷积运算的动机
卷积运算通过三个重要的思想来帮助改进机器学习系统:稀疏交互(sparse interactions)、参数共享(parameter sharing)、等变表示(equivariant representations)。另外,卷积提供了一种处理大小可变的输入的方法。
稀疏交互
卷积网络具有稀疏交互(也叫稀疏连接或者稀疏权重)的特征。
假设一个神经网络中有$m$个输入、$n$个输出。那么对于全连接的矩阵相乘则需要$mn$个参数。如果输出的连接数被设定为$j$个,那么采用稀疏连接则只需要$jn$个参数。在许多情景中,在连接数被设定为$j$,且$j$比$m$要小得多的情况下,机器学习应用的速度获得大幅度的提升,并且仍然能保持较好的效果。
稀疏的图形化解释如图9.2和图9.3所示。在深度卷积网络中,处在网络深层的单元可能与绝大部分输入是间接交互的,如图9.4所示。这允许网络可以通过只描述稀疏交互的基石来高效地描述多个变量的复杂交互。
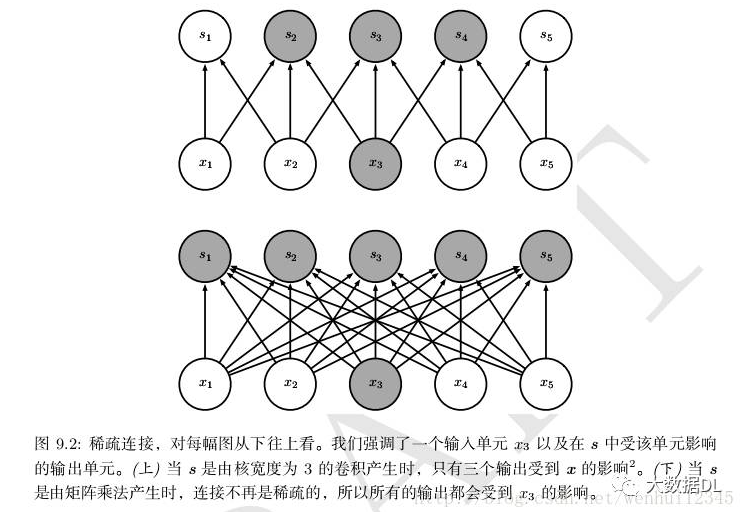
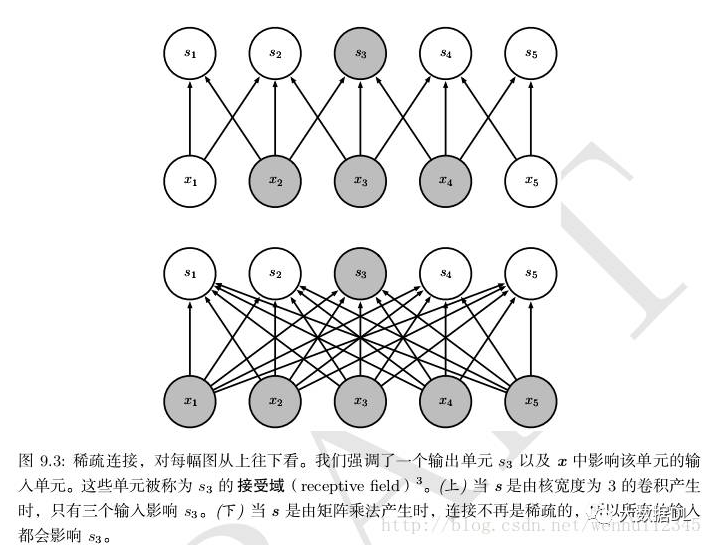
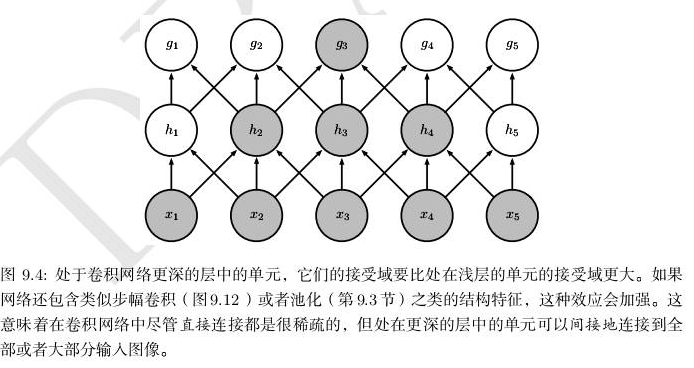
卷积网络通过采用稀疏连接的方法减少了需要存储的参数(权重)的数量,减少了机器学习模型所需要的存储空间,从而提升了模型的统计效率。从计算方面来看,较少的参数数量意味着计算输出时需要更少的参数,从而计算效率也得到大幅提升。
参数共享
参数共享是紧接着稀疏连接而来的,参数共享是指在一个模型的多个函数中使用相同的参数。这个共享的参数通常是权重,即共享权重(Shared Weight)。在传统的神经网络中,每个权重被使用一次。而使用共享权重,一个输入位置的参数值也会被应用在其他的输入位置。在卷积网络中,通过参数共享,一个卷积核内的参数会被应用在输入的所有位置。
下图演示了参数共享时如何实现的。
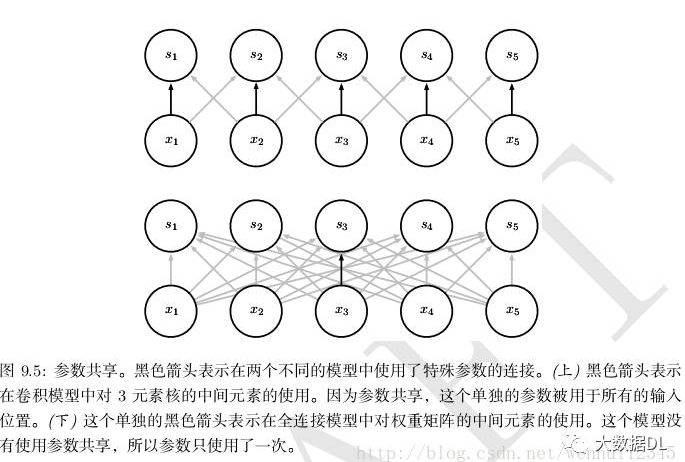
等变表示
对于卷积来说,参数共享的特殊形式使得神经网络层具有了对平移等变(Equivariance)的性质。一个函数满足输入改变,那么输出也以同样的方式改变这一个性质,那么这个函数就是等变的。即输入发生变化输出也相应发生同样的变化。
如果$f(g(x))=g(f(x))$,那么函数$f(x)$对于变换$g$具有等变性。在卷积网络中,令$g$是输入的任意平移函数,那么卷积函数对于$g$具有等变性。
举例,令$I$表示图像在整数坐标上的亮度函数,$g$表示图像函数的变换函数,即把一个图像映射到另一个图像函数的函数。令$I’=g(I)$,图像函数$I’$满足$I’(x,y)=I(x-1,y)$。上述函数所做的变换就是将$I$中的每一个像素均向右移动一个单位。如果先对图像$I$施加变换,再进行卷积操作$f$,结果等同于对图像$I$的卷积施加变换。也就是说,如果图像中的目标发生了一定的位移之后,卷积输出的表达也会产生相同的位移。这个特征对于作用在一个相对小区域的算子十分有用。
卷积运算的计算
二维卷积
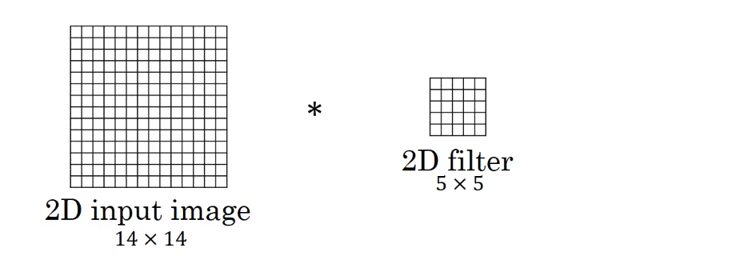
图中的输入的数据维度为$14×14$,过滤器大小为$5×5$,二者做卷积,输出的数据维度为$10×10(14−5+1=10)$。
上述内容没有引入$channel$的概念,也可以说$channel$的数量为$1$。如果将二维卷积中输入的$channel$的数量变为$3$,即输入的数据维度变为$(14×14×3)$。由于卷积操作中过滤器的$channel$数量必须与输入数据的$channel$数量相同,过滤器大小也变为$5×5×3$。在卷积的过程中,过滤器与数据在$channel$方向分别卷积,之后将卷积后的数值相加,即执行$10×10$次$3$个数值相加的操作,最终输出的数据维度为$10×10$。
以上都是在过滤器数量为$1$的情况下所进行的讨论。如果将过滤器的数量增加至$16$,即$16$个大小为$10×10×3$的过滤器,最终输出的数据维度就变为$10×10×16$。可以理解为分别执行每个过滤器的卷积操作,最后将每个卷积的输出在第三个维度($channel$ 维度)上进行拼接。
二维卷积常用于计算机视觉、图像处理领域。
一维卷积
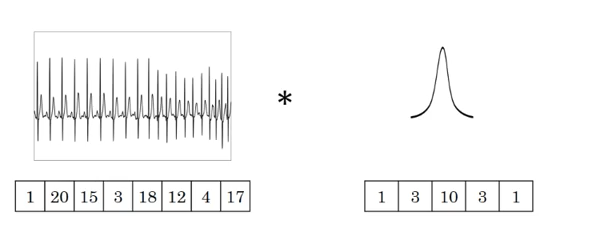
图中的输入的数据维度为$8$,过滤器的维度为$5$。与二维卷积类似,卷积后输出的数据维度为$8−5+1=4$。
如果过滤器数量仍为$1$,输入数据的$channel$数量变为$16$,即输入数据维度为$8×16$。这里$channel$的概念相当于自然语言处理中的embedding,而该输入数据代表$8$个单词,其中每个单词的词向量维度大小为$16$。在这种情况下,过滤器的维度由$5$变为$5×16$,最终输出的数据维度仍为$4$。
如果过滤器数量为$n$,那么输出的数据维度就变为$4×n$。
一维卷积常用于序列模型,自然语言处理领域。
三维卷积
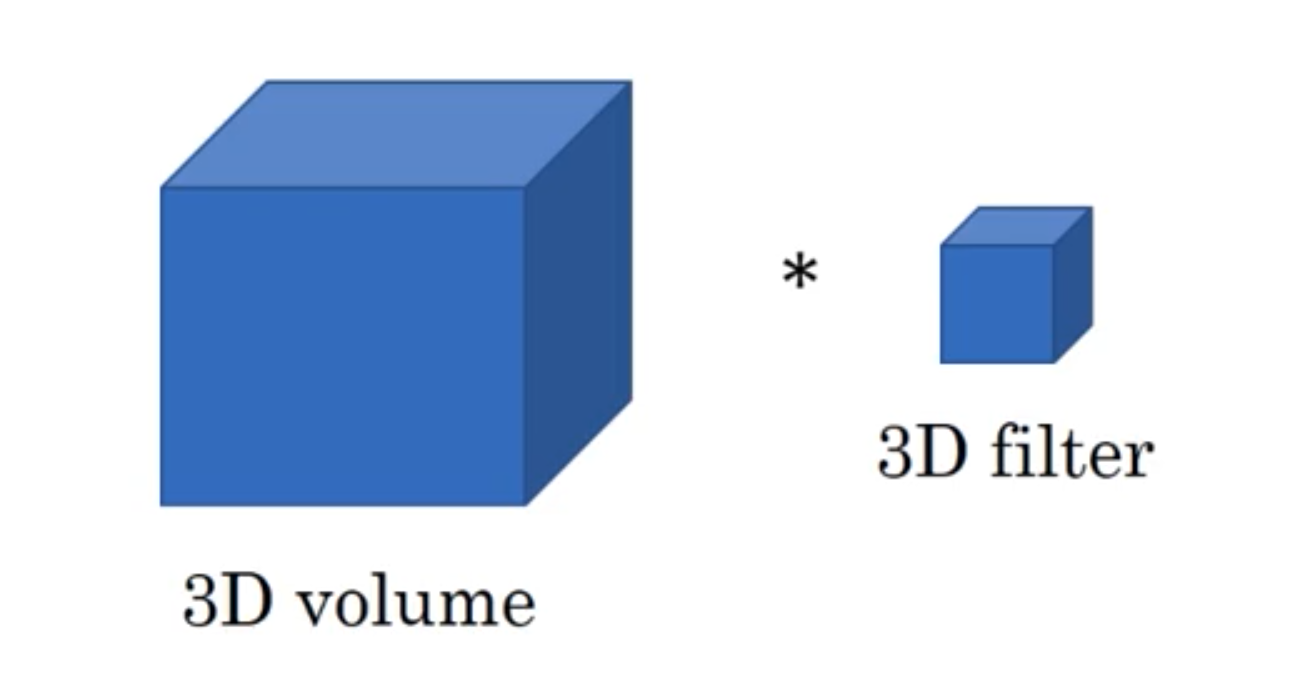
这里采用代数的方式对三维卷积进行介绍,具体思想与一维卷积、二维卷积相同。
假设输入数据的大小为$a_1×a_2×a_3$,$channel$数为$c$,过滤器大小为$f$,即过滤器维度为$f×f×f×c$(一般不写$channel$的维度),过滤器数量为$n$。
基于上述情况,三维卷积最终的输出为$(a_1−f+1)×(a_2−f+1)×(a_3−f+1)×n$。该公式对于一维卷积、二维卷积仍然有效,只有去掉不相干的输入数据维度就行。
三维卷积常用于医学领域(CT影响),视频处理领域(检测动作及人物行为)。
反卷积(tf.nn.conv2d_transpose)
反卷积(Deconvolution)又称为 Transposed Convolution,其实卷积层的前向传播过程就是反卷积层的反向传播过程,卷积层的反向传播过程就是反卷积层的前向传播过程。
池化运算
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。例如:对于一个 $96X96$ 像素的图像,假设我们已经学习得到了$400$个定义在$8X8$输入上的特征,每一个特征和图像卷积都会得到一个$ (96 − 8 + 1) (96 − 8 + 1) = 7921 $维的卷积特征,由于有$ 400$ 个特征,所以每个样例 (example) 都会得到一个$ 892 400 = 3,168,400$ 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,并且容易出现过拟合 (over-fitting)。
之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling),有时也称为平均池化或者最大池化 (取决于计算池化的方法)。
pooling层对filters的抽取结果进行降维操作,获得样本的重要特征,为下一次的卷积增加感受野的大小,逐渐减小"分辨率", 为最后的全连接做准备。pooling层是CNN中用来减小尺寸,提高运算速度的,同样能减小噪声的影响,让各特征更具有健壮性。降维操作方式的不同产生不同的池化方法。一般在pooling层之后连接全连接神经网络,形成最后的分类结果。
池化运算的种类
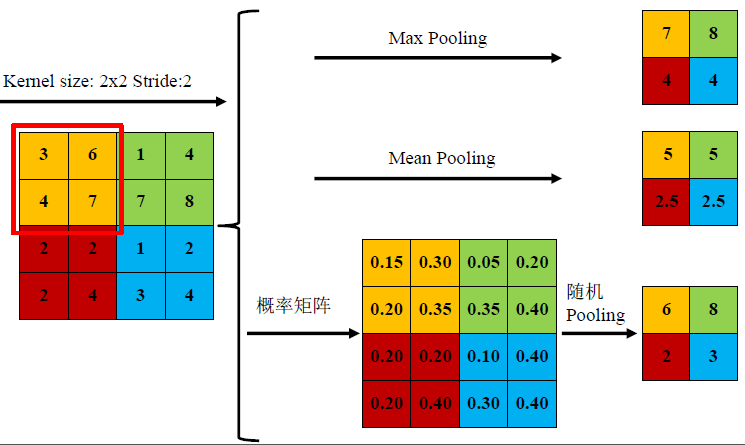
常用的有mean-pooling,max-pooling和Stochastic-pooling三种。
mean-pooling
mean-pooling,即对邻域内特征点只求平均,对背景保留更好。
max-pooling
max-pooling,即对邻域内特征点取最大,对纹理提取更好。
Stochastic-pooling
Stochastic-pooling,介于两者之间,通过对像素点按照数值大小赋予概率,再按照概率进行亚采样。
池化的作用
- 保留主要特征的同时减少参数(降低纬度,类似PCA)和计算量,防止过拟合
- invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度)
translation invariance (平移):
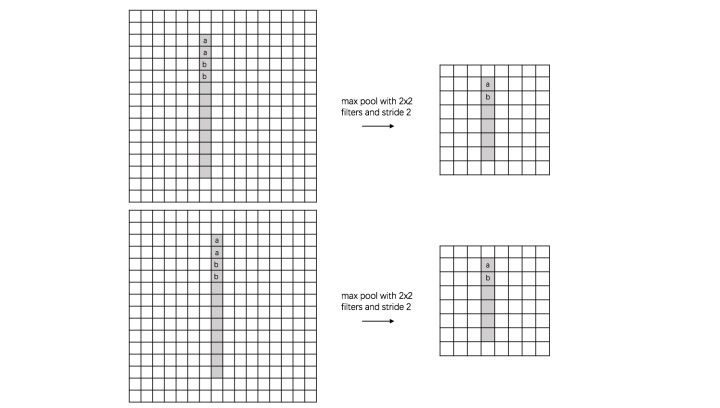
这里举一个直观的例子(数字识别),假设有一个16x16的图片,里面有个数字1,我们需要识别出来,这个数字1可能写的偏左一点(图1),这个数字1可能偏右一点(图2),图1到图2相当于向右平移了一个单位,但是图1和图2经过max pooling之后它们都变成了相同的$8x8$特征矩阵,主要的特征我们捕获到了,同时又将问题的规模从$16x16$降到了$8x8$,而且具有平移不变性的特点。图中的a(或b)表示,在原始图片中的这些a(或b)位置,最终都会映射到相同的位置。
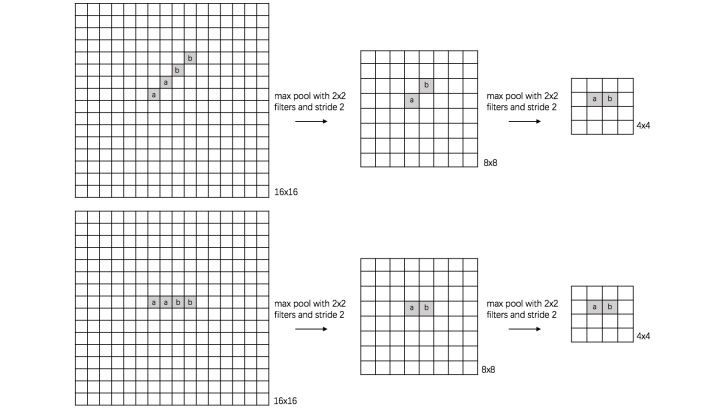
rotation invariance (旋转):
下图表示汉字“一”的识别,第一张相对于x轴有倾斜角,第二张是平行于x轴,两张图片相当于做了旋转,经过多次max pooling后具有相同的特征。
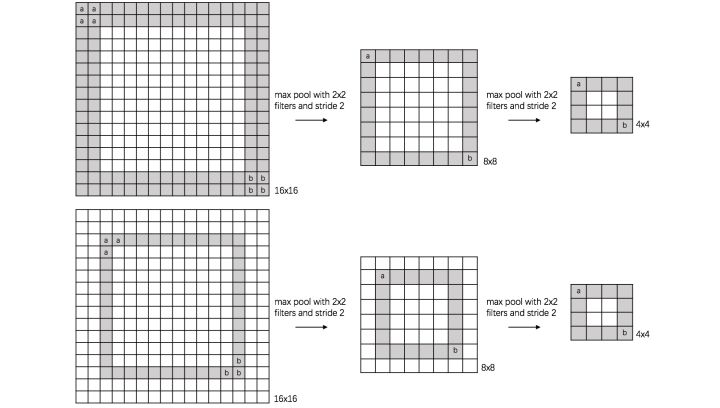
scale invariance (尺度):
下图表示数字“0”的识别,第一张的“0”比较大,第二张的“0”进行了较小,相当于作了缩放,同样地,经过多次max pooling后具有相同的特征。
Text-CNN的原理
网络结构
整个模型由四部分构成:输入层、卷积层、池化层、全连接层。
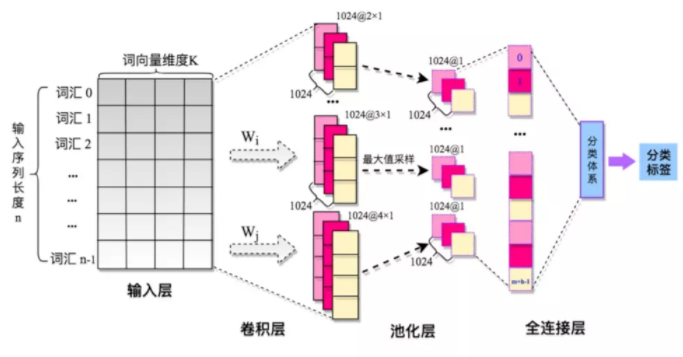
输入层/嵌入层(embedding layer)
Text-CNN模型的输入层需要输入一个定长的文本序列,需要通过分析语料集样本的长度指定一个输入序列的长度$L$,比$L$短的样本序列需要填充(自己定义填充符),比$L$长的序列需要截取。最终输入层输入的是文本序列中各个词汇对应的分布式表示,即词向量。
几个变种的词向量的表达方式:
- static(静态词向量)
使用预训练的词向量,即利用word2vec、fastText或者Glove等词向量工具,在开放领域数据上进行无监督的学习,获得词汇的具体词向量表示方式,拿来直接作为输入层的输入,并且在TextCNN模型训练过程中不再调整词向量, 这属于迁移学习在NLP领域的一种具体的应用。 - non-static(非静态词向量)
预训练的词向量+ 动态调整 , 即拿word2vec训练好的词向量初始化, 训练过程中再对词向量进行微调。 - multiple channel(多通道)
借鉴图像中的RGB三通道的思想, 这里也可以用 static 与 non-static 两种词向量初始化方式来搭建两个通道。 - CNN-rand(随机初始化)
指定词向量的维度embedding_size后,文本分类模型对不同单词的向量作随机初始化, 后续有监督学习过程中,通过BP的方向更新输入层的各个词汇对应的词向量。
卷积(convolution)
在NLP领域一般卷积核只进行一维的滑动,即卷积核的宽度与词向量的维度等宽,卷积核只进行一维的滑动。
在Text-CNN模型中一般使用多个不同尺寸的卷积核。卷积核的高度,即窗口值,可以理解为N-gram模型中的N,即利用的局部词序的长度,窗口值也是一个超参数,需要在任务中尝试,一般选取2-8之间的值。
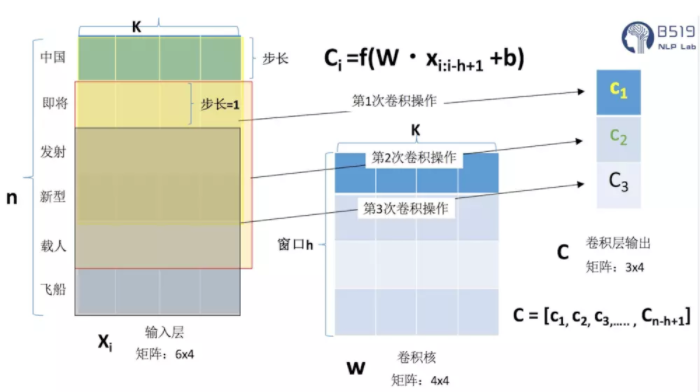
池化(pooling)
在Text-CNN模型的池化层中使用了Max-pool(最大值池化),即减少模型的参数,又保证了在不定长的卷基层的输出上获得一个定长的全连接层的输入。
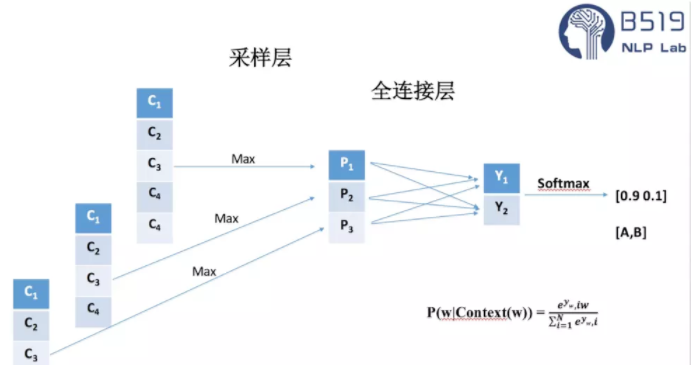
池化层除了最大值池化之外,也有论文讨论过 Top K最大值池化,即选取每一个卷积层输出的Top k个最大值作为池化层的输出。
卷积层与池化层在分类模型的核心作用就是提取特征,从输入的定长文本序列中,利用局部词序信息,提取初级的特征,并组合初级的特征为高级特征,通过卷积与池化操作,省去了传统机器学习中的特征工程的步骤。
但TextCNN的一个明显缺点就是,卷积、池化操作丢失了文本序列中的词汇的顺序、位置信息,比较难以捕获文本序列中的否定、反义等语义信息。
全连接层
全连接层的作用就是分类器,原始的Text-CNN模型使用了只有一层隐藏层的全连接网络,相当于把卷积与池化层提取的特征输入到一个LR分类器中进行分类。
TextCNN的详细过程原理图如下:
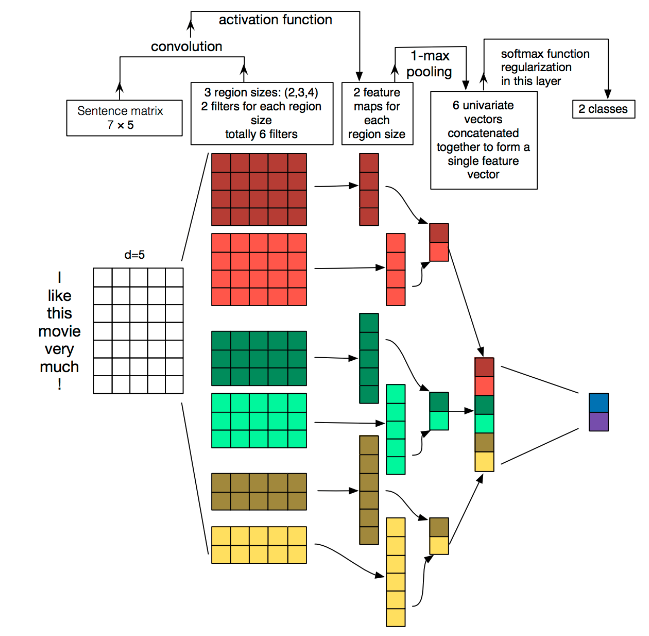
TextCNN详细过程:
- Embedding:第一层是图中最左边的 $7 \times 5$ 的句子矩阵,每行是词向量,维度为$5$,这个可以类比为图像中的原始像素点。
- Convolution:然后经过 $kernel_sizes=(2,3,4)$ 的一维卷积层,每个 $kernel_size$ 有两个输出 $channel$。
- MaxPolling:第三层是一个$1-max pooling$ 层,这样不同长度句子经过 $pooling$ 层之后都能变成定长的表示。
- Full-Connection and Softmax:最后接一层全连接的 $softmax$ 层,输出每个类别的概率。
利用Text-CNN模型来进行文本分类
数据处理
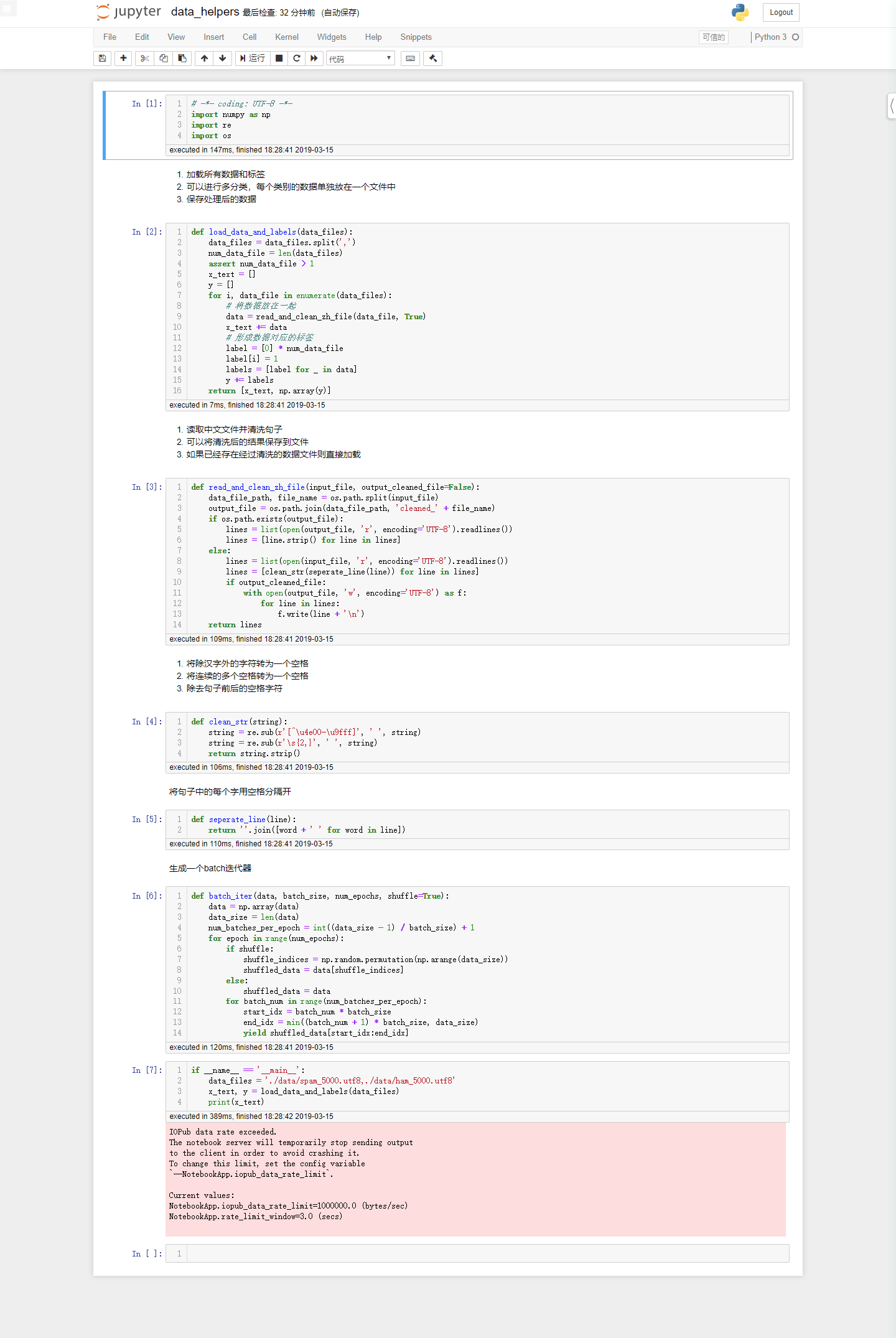
模型
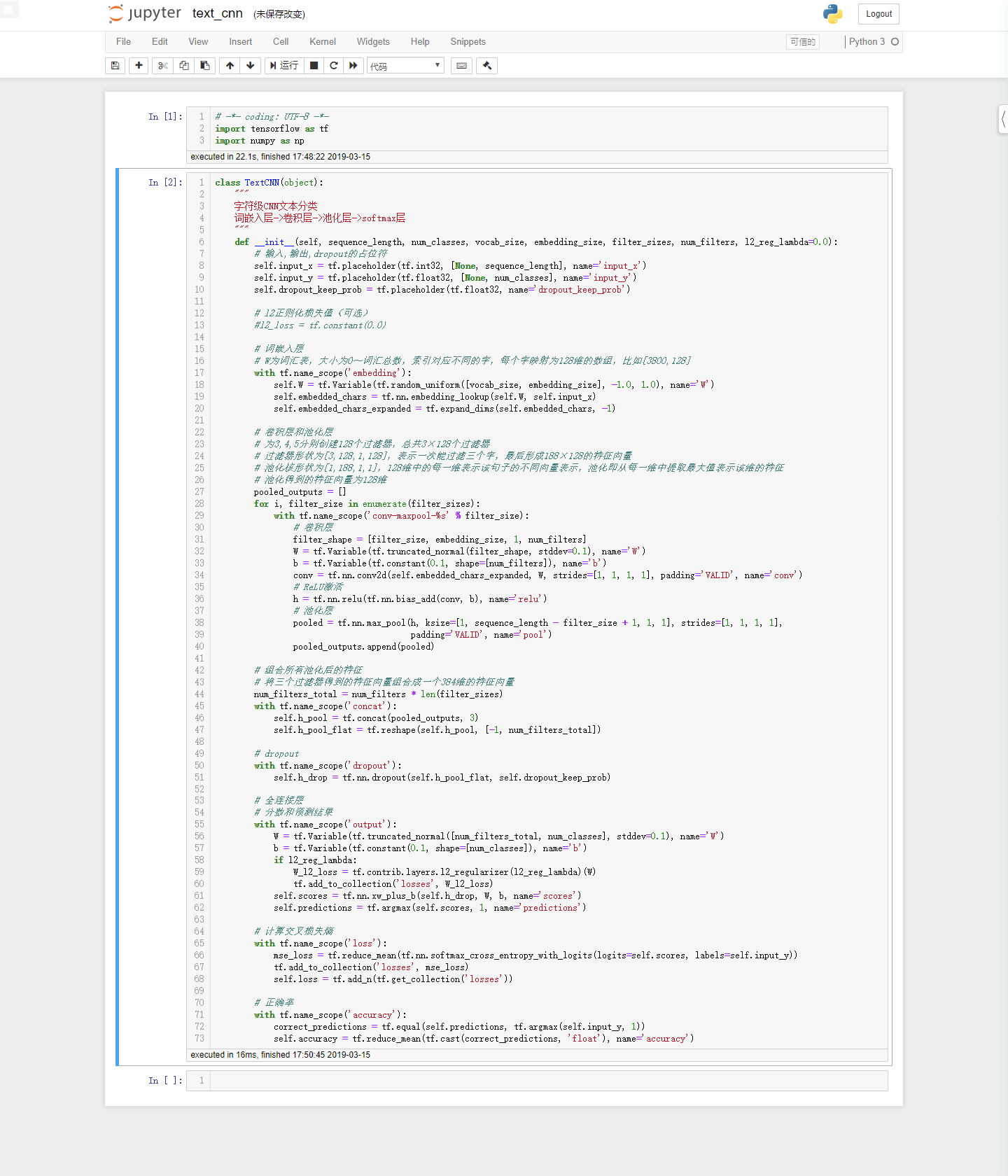
训练
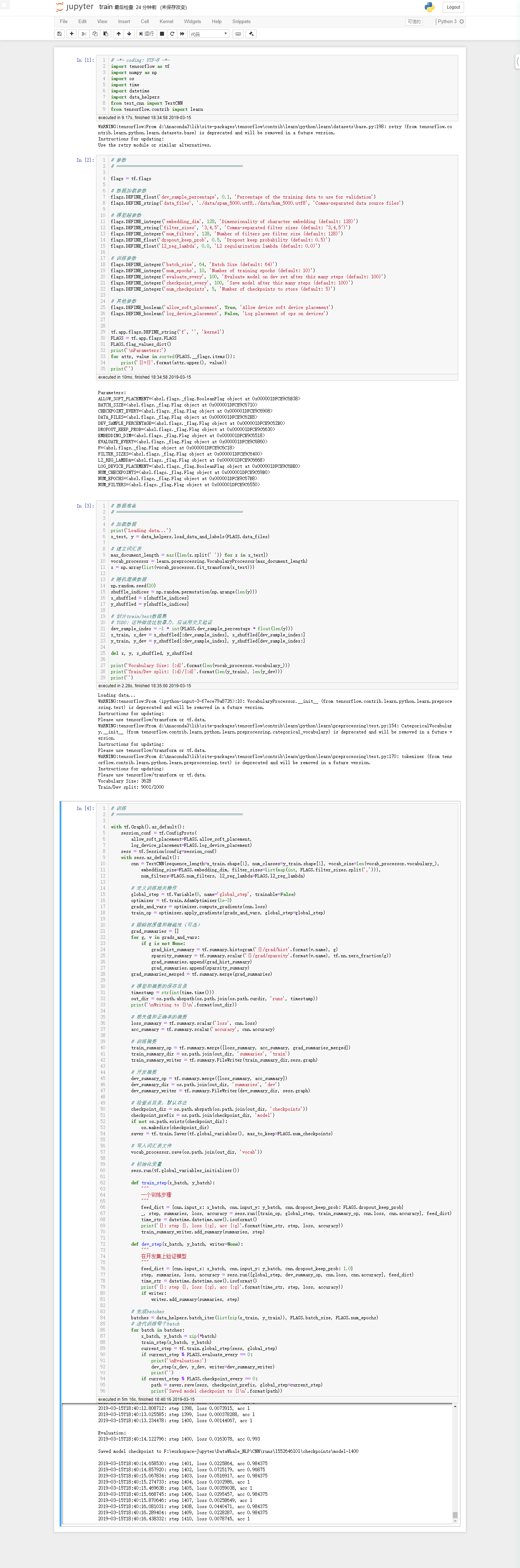
评估