传统机器学习

朴素贝叶斯的原理

贝叶斯分类是一类分类算法的总称，这类算法均已贝叶斯定理为基础，故统称为贝叶斯分类。
公式如下：

$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$

该公式最大的优点就是可以忽略AB的联合概率直接求其条件概率分布。
因为整个形式化过程只做最原始、最简单的建设：各特征属性是条件独立的：

$P(x|y_i)P(y_i) = P(a_1|y_i)P(a_2|y_i).......P(a_n|y_i)P(y_i)$

所以称为“朴素”。

优点：在数据较少的情况下仍然有效，可以处理多类别问题

缺点：对于输入数据的准备方式较为敏感

利用朴素贝叶斯模型进行文本分类

from sklearn import naive_bayes
from sklearn.model_selection import train_test_split
from sklearn import datasets
import pandas as pd

def getData():
    iris = datasets.load_iris()
    X = iris.data  #样本特征矩阵，150*4矩阵，每行一个样本，每个样本维度是4
    y = iris.target  #样本类别矩阵，150维行向量，每个元素代表一个样本的类别

    df = pd.DataFrame(X, columns=['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm'])
    df['target'] = y

    return df

1 2	df = getData() df.head()

	SepalLengthCm	SepalWidthCm	PetalLengthCm	PetalWidthCm
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

X_train, X_test, y_train, y_test = train_test_split(
    df.iloc[:, 0:4], df['target'], test_size=0.3, random_state=42)
print(X_train.head())
print()
print(X_test.head())
print()
print(y_train.head())
print()
print(y_test.head())

     SepalLengthCm  SepalWidthCm  PetalLengthCm  PetalWidthCm
81             5.5           2.4            3.7           1.0
133            6.3           2.8            5.1           1.5
137            6.4           3.1            5.5           1.8
75             6.6           3.0            4.4           1.4
109            7.2           3.6            6.1           2.5

     SepalLengthCm  SepalWidthCm  PetalLengthCm  PetalWidthCm
73             6.1           2.8            4.7           1.2
18             5.7           3.8            1.7           0.3
118            7.7           2.6            6.9           2.3
78             6.0           2.9            4.5           1.5
76             6.8           2.8            4.8           1.4

81     1
133    2
137    2
75     1
109    2
Name: target, dtype: int32

73     1
18     0
118    2
78     1
76     1
Name: target, dtype: int32

model = naive_bayes.GaussianNB()
model.fit(X_train, y_train)
predict = model.predict(X_test)

print(predict - y_test.values)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0]

count = 0
for i in range(len(predict)):
    if predict[i] == y_test.values[i]:
        count += 1
score = float(count) / len(predict)

print('贝叶斯准确率: %3f' % (score))
print('贝叶斯模型得分: {:.3f}'.format(model.score(X_test, y_test)))

贝叶斯准确率: 0.977778
贝叶斯模型得分: 0.978

SVM的原理

定义在特征空间上的间隔最大的线性分类器，可以通过核技巧，变成非线性分类器。

优点：泛化错误率低，计算开销不大，结果易解释

缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于二分类问题

点到超平面的距离：

$distance = \frac{|w^Tx + b|}{||w||}$

找到具有最小间隔的数据点，再对该间隔最大化：

$\mathop{\arg\max}_{(w,b)}\{\min_n \ label·\frac{(w^Tx+b)}{||w||}\}$

转化后的优目标函数：

$\begin{align} \max_\alpha[\sum_{i=1}^m\alpha-\frac{1}{2}\sum_{i,j=1}^{m}&label^{(i)}·label^{(j)}·\alpha_i·\alpha_j·<x^{(i)},x^{(j)}>] \\\\ st. \ &\alpha\geq0\\ &\sum_{i-1}^m\alpha_i·label^{(i)}=0 \end{align}$

引入松弛变量后约束条件变为：

$\begin{align} st. \ &C\geq\alpha\geq0\\&\sum_{i-1}^m\alpha_i·label^{(i)}=0 \end{align}$

利用SVM模型进行文本分类

from sklearn import svm
from sklearn.model_selection import train_test_split
from sklearn import datasets
import pandas as pd

def getData():
    iris = datasets.load_iris()
    X = iris.data  #样本特征矩阵，150*4矩阵，每行一个样本，每个样本维度是4
    y = iris.target  #样本类别矩阵，150维行向量，每个元素代表一个样本的类别

    df = pd.DataFrame(X, columns=['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm'])
    df['target'] = y

    return df

1
2
3

df = getData()
# 效果太好，只取前两个属性
X_train, X_test, y_train, y_test = train_test_split(df.iloc[:, 0:2], df['target'], test_size=0.3, random_state=42)

model = svm.SVC()
model.fit(X_train, y_train)
predict = model.predict(X_test)

print(predict - y_test.values)

[ 0  0  0  0  1  0  0  0  0  0  0  0  0  0  0  1  0  0  0  0  0 -1  0  0
  0  0  0  0  0  0  0  0  1  0  0 -1  1  0  0  0 -1  1  1  0  0]

count = 0
for i in range(len(predict)):
    if predict[i] == y_test.values[i]:
        count += 1
score = float(count) / len(predict)

print('SVM准确率: %3f' % (score))
print('SVM模型得分: {:.3f}'.format(model.score(X_test, y_test)))

SVM准确率: 0.800000
SVM模型得分: 0.800

pLSA、共轭先验分布

LSA（Latent semantic analysis，隐性语义分析）

对词-文档共现矩阵进行 SVD，从而得到词和文档映射到抽象出的 topic 上的向量表示。

LSA 通过将词映射到 topic 上得到 distributional representation（词的分布表示），进而缓解文档检索、文档相似度计算等任务中所面临的同义词（多词一义）问题。

LSA 这种将词映射到 topic 上的向量表示，很难去应对一词多义问题

pLSA（Probabilistic latent semantic analysis，概率隐性语义分析）

pLSA 模型是有向图模型，将主题作为隐变量，构建了一个简单的贝叶斯网络，采用EM算法估计模型参数。相比于 LSA 略显“随意”的 SVD，pLSA 的统计基础更为牢固。

相比于 LDA 模型里涉及先验分布，pLSA 模型相对简单：观测变量为文档 $d_m\in D$ （文档集共 $M$ 篇文档）、词 $w_n\in W$ （设词汇表共有 $V$ 个互不相同的词），隐变量为主题 $z_k\in Z$ （共 $K$ 个主题）。在给定文档集后，我们可以得到一个词-文档共现矩阵，每个元素 $n(d_m,w_n)$ 表示的是词 $w_n$ 在文档 $d_m$ 中的词频。

pLSA 模型也是基于词-文档共现矩阵的，不考虑词序。

pLSA 模型通过以下过程来生成文档（记号里全部省去了对参数的依赖）：

以概率 $P(d_m)$ 选择一篇文档 $d_m$
以概率 $P(z_k|d_m)$ 得到一个主题 $z_k$
以概率 $P(w_n|z_k)$ 生成一个词 $w_n$

概率图模型如下所示:

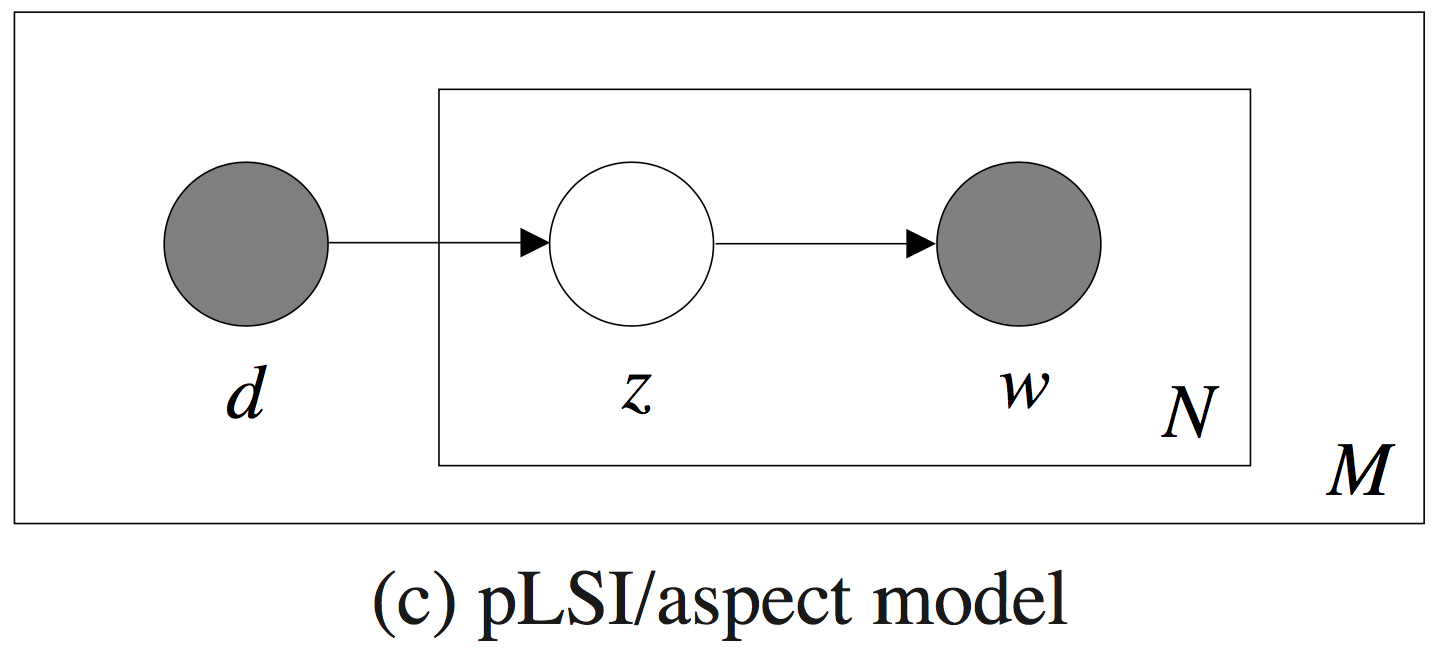
图里面的浅色节点代表不可观测的隐变量，方框是指变量重复，内部方框表示的是文档 $d_m$ 的长度是 $N$，外部方框表示的是文档集共 $M$ 篇文档。pLSA 模型的参数 $\theta$ 显而易见就是：$K×M$ 个 $P(z_k|d_m)$ 、$V×K$ 个 $P(w_n|z_k)$ 。$P(z_k|d_m)$ 表征的是给定文档在各个主题下的分布情况，文档在全部主题上服从多项式分布（共 M 个）；$P(w_n|z_k)$ 则表征给定主题的词语分布情况，主题在全部词语上服从多项式分布（共 $K$ 个）。

共轭先验分布

用于计算后验概率的式子：

$\pi(\theta|x)=\frac{h(x,\theta)}{m(x)}=\frac{p(x|\theta)\pi(\theta)}{\int_\theta p(x|\theta)\pi(\theta)d\theta}$

有时我们将 $p(x|\theta)$ 称为似然函数，先验概率 $pi(\theta)$ 和似然函数的乘积，然后归一化得到后验概率 $p(\theta|x)$。共轭先验的定义为：如果后验概率分布和先验概率分布有相同的形式(如同为指数族分布)，则后验概率分布和先验概率分布统称共轭分布。那么先验概率 $\pi(\theta)$ 称为似然函数的共轭先验。

LDA主题模型原理

LDA（Latent Dirichlet allocation，隐狄利克雷分配）

LDA 将模型参数视作随机变量，将多项式分布的共轭先验（也就是 Dirichlet分布）作为参数的先验分布，并使用Gibbs sampling方法对主题进行采样。

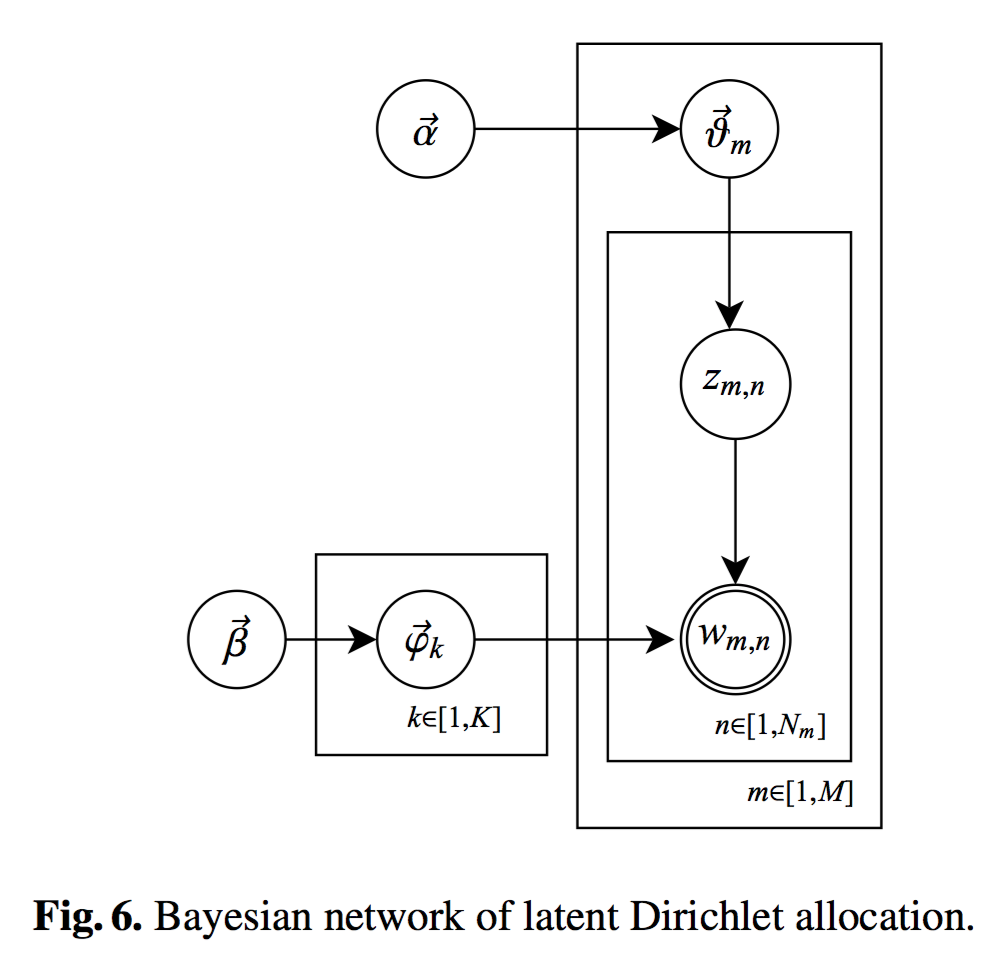
使用LDA生成主题特征，在之前特征的基础上加入主题特征进行文本分类

参考资料
NLP —— 图模型（三）pLSA（Probabilistic latent semantic analysis，概率隐性语义分析）模型
 深入浅出讲解LDA主题模型